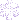usando el dibujo, calcule cuantos caminos eran posibles pasando por la calle bloqueada y me dieron 10296, ya que desde el punto inferior de la calle bloqueada hasta el destino hay 14 movidas totales y 7 hacia abajo, y usando los cualculos, me dio:3432 caminos, solo que contando la cantidad de posibles caminos de el punto de salida hasta la calle cortada son 3, y por lo tanto es 3x3432=10296
por otra parte, hice lo mismo con la avenida cortada, y me dio: 56 caminos desde la salida hasta la avenida cortada. Ademas, desde el final de la avenida cortada hasta el punto de llegada son 126 caminos. al hacer 126x56 me da que 7056 no se pueden hacer a causa de la avenida cortada.
Sin embargo, de ambos resultados, hay camino que se repiten. Para eso, debo calcular cuantos caminos pasan por la calle y la avenida cortada. Este valor sería 12 posibles caminos hasta la avenida, multiplicados por los 126 que hay desde la avenida hasta el destino, siendo en total 1512 caminos que se repiten.
Entonces, con el valor que dio pablo calculamos cuantos caminos posibles SE PUEDEN hacer:
48620-(10296+7056-1512)=32780 caminos posibles totales.
Espero que este bien!!
Sldos,
Tom